Decíamos en la entrada anterior que fue hace ya más de 2.250 años cuando tuvo lugar el gran acontecimiento científico que demostró la redondez de la Tierra y permitió medir por primera vez el tamaño del globo terrestre. Esta proeza fue realizada por Eratóstenes de Cirene gracias a su célebre experimento de la medida de la circunferencia de La Tierra. Esta medida, que de forma sorprendentemente adelantada a su tiempo sigue las pautas del moderno método científico y pone las matemáticas al servicio del conocimiento de la naturaleza, es considerada justamente por muchos como uno de los experimentos más bellos y trascendentales de la Historia de la Ciencia.
Pero ¿quién era Eratóstenes?
Eratóstenes nació en Cirene alrededor del año 275 a. J.C., lugar en el que comenzó sus estudios de orientación literaria. Se desplazó más tarde a Atenas a completar su formación en el Liceo y en la Academia, donde fue discípulo de Aristóteles entre otros.
Cuando ya gozaba de cierta fama como literato y filósofo, fue llamado por el rey Tolomeo III Everjetes a Alejandría, ciudad donde permanecería hasta el final de su vida. Allí fue encargado de la educación de Filopator, el hijo y sucesor del rey. Fue nombrado sucesivamente Maestre del Museo y Director de la Biblioteca de lejandría, el gran centro del saber de la época helenística. Esto acontecía en el año 255 a. J.C. tras la muerte de Zenodoto, su anterior director, y a este periodo se deben sun principales aportaciones en los campos de las matemáticas y la geografía.
Eratóstenes murió en esta ciudad alrededor del año 193 a. J.C. superando los ochenta años de edad y rodeado de gran prestigio. Se dice que, afectado de ceguera en su vejez, se suicidó al comprender que no podría volver a leer más.
La obra de Eratóstenes
De sus obras científicas tan sólo han llegado a nuestros días fragmentos y resúmenes aportados por otros sabios helenísticos como Papo, Estrabón o Tolomeo (1). Aunque fue Estrabón el que más atención dedicó a los escritos de Eratóstenes, Tolomeo los sintetizó en el Almagesto, junto a los demás conocimientos de la época.
Según algunos autores (Sarton 1970), sus aportaciones al campo de la Geografía estarían incluidas en un tratado “Sobre la medida de la Tierra”, en el que describiría su famoso experimento de la medida del meridiano, y en las “Memorias Geográficas”. Estas memorias constarían de tres partes: Una introducciópn histórica, otra de geografía matemática y una tercera de mapas y geometría descriptiva; y de ellas cabría destacar como principales las aportaciones siguientes:
1.- La medida de los 24º de oblicuidad de la eclíptica y la consiguiente delimitación de zonas geográficas polares y tropicales según su latitud.
2.- Su pensamiento sobre la inmutabilidad de la la esfericidad de la Tierra, estimando insignificantes los accidentes geográficos y las catástrofes geológicas.
3.- Una documentada colección de datos de habitantes y productos naturales de distintos países.
Como se ha dicho antes, Eratóstenes hizo incursiones importantes en otras áreas del Saber. A él se debe un calendario de 365 días y un cuarto (calendario juliano) donde introdujo años bisiestos y trató de situar acontecimientos políticos y culturales. En las Matemáticas es conocido como el creador de la “Criba” que lleva su nombre, algoritmo que permite obtener los números primos, y también como inventor de un aparato de cálculo de proporcionalidades llamado “mesolabio”. Finalmente, ya en un segundo plano, se podrían citar aportaciones suyas a la teoría de la Música, la Poesía o la Filosofía.
El procedimiento para medir la circunferencia de La Tierra
Eratóstenes tuvo conocimiento de que en un lugar del alto Nilo llamado Siena (en la actual ciudad de Asuán), unos 800 km al sur de Alejandría, en el mediodía del solsticio de verano, los rayos del Sol incidían perpendicularmente en el suelo horizontal, hecho que quedaba patente al poder observarse su reflejo en la superficie del agua de un pozo profundo (2). Esto no sucedía así en Alejandría, en donde podía comprobarse en ese momento cómo los rayos de sol incidían oblicuos sobre el suelo llano produciendo sombras.
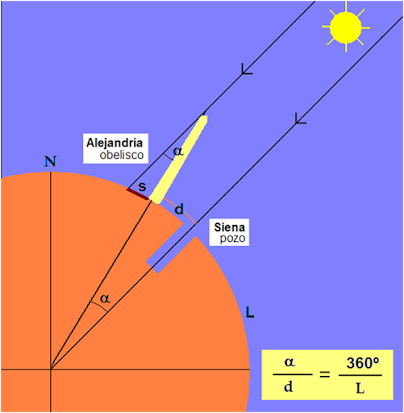
Admitiendo que los rayos del Sol llegan paralelos a la Tierra, dada su lejanía, este hecho sólo sería explicable si la superficie de la Tierra estuviese curvada. Partiendo de la hipótesis más probable de que la curvatura de la Tierra fuera esférica, y sabiendo que los dos lugares alineados en dirección norte-sur pertenecerían a la misma circunferencia (meridiano), Eratóstenes dispuso un método tan sencillo como ingenioso para medir dicha circunferencia y así hallar la verdadera dimensión de la Tierra (ver figura).
El mismo día y a la misma hora en que en Siena los rayos de sol llegaban perpendiculares y alcanzaban lo más hondo del pozo, incidían en Alejandría con una inclinación α proporcional a la longitud d del arco de la circunferencia terrestre que pasa por ambas localidades. Conociendo α y d, y llamando α max al ángulo de la circunferencia completa, la longitud total de la circunferencia terrestre L se puede obtener con una simple relación proporcional (3):
α / α max = d / L
El procedimiento para medir la inclinación del sol α fue colocando un “gnomon”, en esencia un objeto recto de altura h conocida, colocado verticalmente, que proyecta una sombra sobre el suelo horizontal cuya longitud s es proporcional a α. Obtuvo así una medida de α = 1 / 50 de circunferencia (unos 7º 12’)
La distancia d fue estimada en 5000 estadios. No está claro como dio con ese valor. Pudo ser talonada por algún agrimensor o tal vez a partir del tiempo invertido por las caravanas que hacían el viaje entre ambas ciudades.
De este modo, aplicando la proporción 1 / 50 = 5.000 / L , resulta L = 250.000 estadios,
resultado que, según los escritos que relatan su medida, fue corregido por él mismo por el valor:
L = 252.000 estadios
Análisis e importancia de su resultado
A pesar de lo que se dice en algunos libros y artículos que relatan este célebre experimento, lo cierto es que resulta imposible saber con certeza cuál fue la exactitud de esta medida (TATON, 1985)
Existen importantes imprecisiones en el propio procedimiento, tales como la medida de la distancia entre Siena y Alejandría y el hecho de que estas no estén exactamente en el mismo meridiano, sino que haya una diferencia de 3º.
También se desconoce el valor exacto de la unidad de longitud empleada, el estadio, por varias razones. Esta unidad se definía como múltiplo de otras unidades antropomórficas subjetivas como el pie o el codo; además todavía existe la duda de si los 250.000 estadios obtenidos se refieren a estadios griegos (600 pies) o egipcios (300 codos), equivalentes respectivamente y de forma estimada a 185 y 158 metros.
Teniendo en cuenta estas equivalencias se obtendría un resultado de 46.620 km o bien de 36.690 km, frente al valor real medio de 40.120 km que sabemos que tiene la circunferencia terrestre.
Admitiendo en el mejor de los casos que utilizase el estadio egipcio, y que la equivalencia utilizada sea correcta, habría obtenido la medida de la Tierra con una precisión asombrosa con solo un 1 % de error. Sin embargo habría que entender el resultado como una casualidad fruto de errores que se compensan entre sí dentro de un margen amplio de imprecisión (4).
Ante toda esta incertidumbre nos tendremos que conformar con acotar el error de la medida realizada por Eratóstenes entre el 0,5 y el 17% de su valor real, lo que aun en el peor de los casos vendría a ser una aproximación muy estimable, dados los medios a su alcance.
De cualquier manera la gran aportación de Eratóstenes no fue tanto el resultado numérico obtenido como la propia idea y el procedimiento para medir la forma y el tamaño de La Tierra, idea considerada hoy, sin duda, como uno de los grandes hitos de la Historia de la Ciencia.
NOTAS:
(1).- La lista completa de obras atribuidas a Eratóstenes y los fragmentos que de ellas se conservan se encuentran en la “Eratosthenica” de Bernhardy (Berlín, 1822), completada por Hiller en 1872.
(2).- Esto hace pensar que el lugar del pozo debería estar muy próximo a lo que hoy se sabe que es la latitud del trópico de Cáncer. Payer, en el libro “The well of Eratosthenes” sostiene que el referido pozo no estaría exactamente en Siena sino en Elephantina, una la isla del Nilo cercana.
(3).- Parece ser que Eratóstenes utilizaba como grado angular 1/60 de círculo y no 1/360 como solemos utilizar actualmente. De cualquier manera esto es irrelevante al considerar la fracción α / α max
(4).- En la realidad la distancia d entre Siena y Alejandría es de 5.346 estadios egipcios y no los 5.000 que estimó Eratóstenes. Casualmente esa discrepancia es casi igual a la corrección que habría que hacer para solventar la diferencia de 3º de los meridianos de ambos lugares.
FUENTES:
SARTON, G. (1970) A History of Science. Vol 1, 2. Cambridge (Mass.)
TATON, R. (1985) Historia General de las Ciencias. Vol 1. Destino
VV.AA. (1981) The New Encyclopaedia Britannica. Micr.vol.3, macr. Vol.6
VV.AA. (1977) Historia de la Ciencia. Vol.1 Planeta
VV.AA. (1979) El Universo y La Tierra. Vol.1. Labor
VV.AA. (1973) Enciclopedia Universal Ilustrada. Espasa Calpe
No hay comentarios:
Publicar un comentario