La Tierra es redonda (I)

En estos tiempos en los que los terraplanistas conspiranoicos empiezan a ser legión, se me ocurre que es una buena ocasión para reescribir un viejo trabajo sobre la forma y tamaño de la Tierra y, de paso, recordar la medidas del radio del globo terrestre realizadas con mis alumnos. 

 

Ya sabemos que es redonda, pero ¿desde cuándo?

Contrariamente a lo muchos creen, la curvatura de la superficie terrestre y su forma esférica son ideas que vienen de tiempos muy antiguos.

En la cuna de la civilización, los babilonios, pese a sus conocimientos de astronomía pensaban que la Tierra era plana (se ve que todavía queda algún babilonio suelto). Sin embargo, cuesta imaginar que algún observador no se diese cuenta entonces de que la sombra proyectada por la Tierra en un eclipse lunar era circular, o que viajando hacia el sur se verían nuevas estrellas, ocultas bajo el horizonte en su lugar de partida.

Algún autor ha llegado incluso a sugerir que los egipcios que construyeron las pirámides de Guiza (2500 a. de J.C.) ya habrían tenido en cuenta la curvatura de la superficie terrestre en su diseño, aunque esto no parece demasiado probable.

Homero (850 a. J.C.) ya describió la Tierra como un disco convexo, ¡no plano!, como aseguran ahora los terraplanistas, en el que el mundo conocido estaría rodeado por un inmenso océano, mientras que sus contemporáneos seguían creyendo en el mito de origen hindú que describía el mundo como un plato llano y circular sostenido por cuatro elefantes, sostenidos a su vez por una gigantesca tortuga marina. ¿Se habrían preguntado también quién sostenía a la tortuga?

La primera referencia clara a la forma esférica de la Tierra se atribuye a Pitágoras y su escuela (500 a. de J.C.), como la conclusión lógica de que siendo el Sol y la Luna astros de apariencia esférica, también tendría que serlo la Tierra. Esta idea tenía un carácter dogmático, por lo que no gozó de aceptación general entre los pensadores de su época.

Un siglo más tarde, Hiparco y Aristóteles entre otros, apoyaron esta idea. Este último  dedicó parte de su obra “De Caelo” a la defensa de esta doctrina. De este modo, es el propio Aristóteles quien avanza un paso adelante al ser el primero en aportar una estimación del tamaño de la esfera terrestre, a la que asignó un meridiano de 400.000 estadios griegos ( unos 74 000 km), casi el doble de su valor real.

Hay constancia de alguna que otra estimación, que no medida en el sentido estricto del término, Así Arquímedes y Cleomedes establecen  respectivamente 300.000 y 252.000 estadios. A pesar de que estos valores se acercan más al valor real, no suponen una aportación verdaderamente científica, pues no se basan en medida experimental alguna.

 

Y entonces llegó Eratóstenes

La prueba definitiva sobre la forma y el tamaño de la Tierra llegaría a finales del siglo III a. de J.C. de la mano de Eratóstenes de Cirene, por entonces director de la Biblioteca de Alejandría, con su célebre medida del meridiano terrestre. Esta medición, que describiremos detalladamente un poco más adelante, está considerada por muchos como uno de los experimentos más bellos y uno de los mayores logros intelectuales de la historia de la ciencia.

Eratóstenes se planteó zanjar la polémica de la forma de la Tierra motivado posiblemente por la necesidad de confeccionar un mapa universal. Lo que hizo fue poner de manifiesto y comparar la diferente longitud de las sombras proyectadas al mediodía del solsticio de verano, por un gnomon colocado verticalmente sobre el suelo horizontal en dos localidades, Alejandría y Siena, separadas una distancia conocida y una más al sur que la otra. De este modo, y en esto precisamente consiste su genial aportación,  demuestra en primer lugar y de forma experimental la curvatura de la superficie terrestre y, asumiendo su esfericidad, a continuación calcula matemáticamente la longitud de su circunferencia a partir del resultado de este experimento. El resultado obtenido fue de 252.000 estadios (unos 40.000 km aproximadamente), valor de sorprendente exactitud teniendo en cuenta los medios de que disponía.

La segunda determinación que se conoce la hizo Posidonio, griego de Apamea (Siria), un siglo y medio más tarde. Empleó un método parecido, pero basado esta vez en medir la elevación de la estrella Canopus sobre el horizonte desde la isla de Rodas justo la noche en que se veía en el horizonte en Alejandría. Obtuvo un resultado concordante con el de Eratóstenes y que no excedía más de un 11% del valor real.

Después de estos hechos tan evidentes, habría de pasar mucho tiempo hasta que la cultura, tanto la vulgar como la autorizada, reconociese el hecho de la redondez de la Tierra. La lamentable destrucción de la Biblioteca de Alejandría, el desmoronamiento del imperio romano y el asentamiento del cristianismo serían sin duda determinantes en esta cuestión. Recordemos que nada menos que unos dos mil años después de los pitagóricos, todavía se desconfiaba del proyecto de Colón de abrir una ruta por el oeste para viajar a las Indias.

Durante la edad media bastaban simples prejuicios para rechazar cualquier argumento positivo a favor de una Tierra esférica, como por ejemplo asumir la existencia de los llamados “antípodas”, humanoides que vivirían al otro lado del mundo y que estarían obligados a andar con los pies en alto y cabeza abajo. Parece ser que se llegó a calificar de hereje a todo aquel que osase afirmar la existencia de tales seres. No se volvió a hablar de la esfericidad terrestre hasta el final del medievo, gracias a los estudios astronómicos de Copérnico y Galileo.

La resistencia mostrada durante tanto tiempo frente al hecho evidente de la redondez de la Tierra, puede quedar bien  ilustrada sin más que decir que la primera esfera construida para representar el mundo, dibujada por el astrónomo alemán Behaim, data del año 1492.

 

 

 

 

 

 

 

 

El Erdapfel (1942), el globo terráqueo más antiguo en la actualidad, obra de Martin Behaim.

(Germanisches Nationalmuseum, Núremberg)

 

 

El nacimiento de la geodesia  

Con la ilustración del siglo XVIII llega el desarrollo definitivo  de la geodesia, que es la ciencia que estudia la forma y las dimensiones de la Tierra.

Aunque antiguamente ya destacaran los agrimensores romanos, y posteriormente los árabes, que usaban el astrolabio, el cuadrante y la brújula para realizar medidas de terrenos, la geodesia a gran escala alcanzó su plenitud en 1735 gracias a las expediciones científicas  francesas  de Maupertius a Laponia y La Condamine al Ecuador, ésta última con los marinos y científicos españoles Antonio de Ulloa y Jorge Juan a bordo.  En esta misión se establece la medida precisa del meridiano terrestre, a la vez que se confirma la hipótesis de la forma elipsoidal  de la Tierra, midiendo el  achatamiento polar.

Medir con precisión el planeta no es tarea fácil. No se trata de una esfera exacta, su superficie tiene altibajos (montañas, simas) y no es estática (deriva continental, mareas, erosión, volcanes).

La geodesia emplea como métodos fundamentales la triangulación (posición de un cuerpo sobre la superficie), la nivelación (medición de alturas), la astronomía geodésica ( posición de un punto respecto a los astros) y la gravimetría (desviaciones de la vertical). Esta última aprovecha la variación de la gravedad para medir la altitud en determinados puntos de la Tierra. Paralelamente, la geodesia inferior, también llamada geodesia práctica o topografía, representa partes menores de la Tierra donde la superficie puede ser considerada plana.

 

La geodesia moderna revela la forma y el tamaño real de la Tierra

A mediados del siglo XX aparece la geodesia espacial, que utiliza en gran medida los fundamentos matemáticos que ya estaban establecidos para la geodesia tradicional. Con las nuevas tecnologías aparecen nuevas posibilidades y gracias a las técnicas espaciales se puede determinar con gran precisión la forma de la Tierra o las coordenadas de cualquier punto sobre la superficie terrestre. De este modo se comprueban y se miden las desviaciones tanto generales como locales del globo, o mejor dicho, del elipsoide ideal de referencia terrestre y se va revelando el geoide, la verdadera forma de la Tierra.  

La posición precisa de cualquier punto es detectada al instante mediante los sistemas GPS a través de señales de radiofrecuencia entre una constelación de satélites y receptores terrestres.

Las distancias exactas entre puntos e incluso movimientos imperceptibles de los continentes se hacen patentes con métodos de interferometría entre satélites. Por otra parte, las modernas técnicas de gravimetría  de precisión y la red de estaciones gravimétricas permiten medir las pequeñas desviaciones de la regularidad de la superficie de la Tierra y establecer con precisión cuál es su forma y dimensión exacta.

 La geodesia moderna establece con precisión que la Tierra es un elipsoide casi esférico algo deformado irregularmente, cuyo resultado se denomina geoide.

A continuación se precisa la definición de estos conceptos, y se dan los valores  actuales del radio y la  gravedad terrestre:

 

Valores del radio y la gravedad de la Tierra

Masa:                                    5,974.10²⁴ kg

Radio polar:                            6356,7 km

Radio ecuatorial:                     6378,1 km

Radio medio:                          6371,0 km

Gravedad polar:                       9,832 m /s²

Gravedad ecuatorial:                9,780 m/s²

Gravedad media:                     9,806 m/s²

Gravedad local (Logroño):         9,802 m/s²

Densidad media:                     5115 kg/m³

 

 

 

Geoide: Forma teórica de la Tierra real. Se define como la superficie terrestre donde la gravedad toma el mismo valor. Se toma como nivel cero a partir del cual se miden las altitudes. Coincide con el nivel medio del mar, y en los continentes se calcula de manera indirecta.

Elipsoide terrestre: Esfera achatada por los polos obtenida por rotación de una elipse sobre el eje de rotación terrestre. Es la figura regular más aproximada al geoide, y por lo tanto a la forma auténtica de la Tierra. Se utiliza como superficie de referencia para fijar las coordenadas (longitud y latitud) de cualquier punto de su superficie.

 

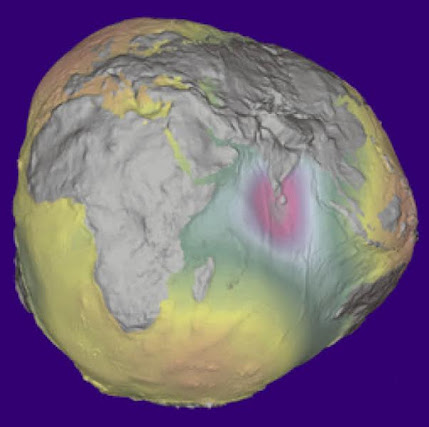
Imagen realzada del geoide terrestre (GFZ. Helmholtz Centre. Postdam)

 

En conclusión. Gracias a la geodesia moderna hoy sabemos que la Tierra no es exactamente una esfera, ni siquiera un elipsoide perfecto, sino un geoide con irregularidades, cuyo radio aproximado es de unos  6370 km. Así pues, La Tierra no es exactamente como una naranja ni siquiera tampoco como una mandarina. La Tierra es más bien ¡como una pera!, aunque eso sí, una pera muy redonda y un poco achatada.

 

 

 

 

 

La paradoja de los gemelos también es relativa

 

Pues sí, como es fácil de adivinar, este artículo trata de la teoría de la relatividad.

El desarrollo de esta teoría suele dar lugar a conclusiones sorprendentes que desafían abiertamente a la idea del espacio y del tiempo que tenemos comúnmente arraigada en nuestra mente. Una de las más conocidas es la famosa “paradoja de los gemelos”

Se dice que esta paradoja fue planteada por primera vez por  P. Langevin a A. Einstein, poco después de que éste publicara  la Teoría de la Relatividad Especial en 1905, alertando de de su posible incongruencia, pues llegaba a predecir situaciones absurdas o contradictorias.

Realmente,  la teoría de la relatividad no sólo no contradice a los hechos observables sino que supera a la mecánica clásica tanto en la justificación como en la predicción de los mismos. Como vamos a ver, la paradoja tiene solución, aunque el propio Einstein no la resolvería definitivamente hasta formular la Teoría de la Relatividad General unos 10 años después.

Aunque la analizaremos después más a fondo, la paradoja de los gemelos surge de un experimento mental que consiste básicamente en lo siguiente:

Un joven astronauta parte de la Tierra para hacer un largo viaje de ida y vuelta a un astro muy lejano en una nave que alcanza una velocidad constante muy próxima a la velocidad de la luz. Su hermano gemelo se queda en la Tierra esperando el día de su regreso, que se producirá dentro de algunos años.

Según las leyes relativistas, un observador que midiera la longitud y el tiempo transcurrido entre dos sucesos que tuviesen lugar en un cuerpo moviéndose con cierta velocidad con respecto a él, obtendría resultados distintos a los que mediría si los viese en reposo. Concretamente, la longitud se contrae y el tiempo se dilata. Este efecto es tanto más notable cuanto más se aproxime a la velocidad de la luz la velocidad del cuerpo con respecto al observador.

Según esto, el gemelo en la Tierra observaría que el tiempo real transcurre más despacio a bordo de la nave que el suyo propio. Como resultado de ello, al producirse el reencuentro tras el largo viaje, el gemelo de la Tierra, envejecido con el paso de los años, contemplaría cómo su hermano viajero, que asegura haber pasado muchos menos años de viaje, es mucho más joven que él.

Pero por extraño que parezca, la cosa no termina aquí. La auténtica paradoja surge si ahora planteamos el viaje desde el punto de vista del gemelo que va en la nave:

De acuerdo con su marco de referencia es La Tierra con su hermano esperando en ella la que se mueve con respecto a la nave con la velocidad citada. Así que el gemelo astronauta, para quien el tiempo pasa con total normalidad, observaría cómo en la Tierra el tiempo pasa más despacio. Cuando al fin del viaje se encuentre con su hermano en la Tierra, ¡el astronauta confirmaría que su gemelo es bastante más joven que él!

Entonces ¿envejece más el gemelo que espera o el gemelo que viaja? La aplicación, aparentemente correcta, de la teoría de la relatividad especial llega al absurdo de dar dos respuestas contradictorias para un único fenómeno real. Ésta es la verdadera paradoja.

 

El 27 de marzo de 2015 La NASA realizó un experimento en el que participaron los dos hermanos gemelos de la foto. El astronauta Scott Kelly pasó exactamente un año en órbita a bordo de la Estación Espacial Orbital mientras su hermano Mark permanecía en La Tierra haciendo su vida normal. El objetivo era comparar las consecuencias genéticas, físicas y cognitivas de una larga estancia en el espacio. Aunque algunos han querido ver en esta misión un guiño a la famosa paradoja de los gemelos, lo cierto es que la velocidad de la ISS con respecto a la Tierra está muy lejos de ser suficiente como para poder detectar diferencia alguna en la edad final de los dos hermanos. (foto NASA)

 

 El espacio y el tiempo según la Teoría de la Relatividad Especial

Antes de analizar más detenidamente el problema de los gemelos sería conveniente recordar, aunque sea muy resumidamente, en qué se basa la teoría de la relatividad y qué consecuencias tiene en la medida del espacio y del tiempo.

Con el fin de explicar ciertos hechos experimentales relacionados con la propagación de la luz y otros fenómenos electromagnéticos al ser observados desde distintos marcos de referencia, A. Einstein formula en 1905 la Teoría de la Relatividad Especial o Restringida como una nueva teoría del movimiento deducida a partir de dos postulados que asumen sendas evidencias experimentales, y que se aplica exclusivamente a observadores en sistemas de referencia sin ningún tipo de aceleración (sistemas de referencia inerciales). Estos postulados son:

1-    No hay ninguna cualidad que permita distinguir si un sistema de referencia está en reposo o en movimiento rectilíneo y uniforme. En consecuencia, las leyes de la física tienen que ser las mismas independientemente del sistema de referencia inercial que las formule.

2-    La velocidad de la luz en el vacío (c) es invariante, independientemente de la velocidad y dirección del observador inercial que la mida.

Como consecuencia de ellos, se deducen varias leyes que, a pesar de contradecir aparentemente el sentido común, resultan ser más coherentes con los hechos experimentales que la mecánica clásica. Estas consecuencias afectan a la noción que hasta entonces se tenía de conceptos y magnitudes como el espacio, el tiempo, la simultaneidad de sucesos, la velocidad, la masa, el momento lineal o la energía; los relativiza haciéndolos dependientes unos de otros y del observador que los describe, superando a la mecánica clásica, con la que coincide cuando la velocidades de los observadores son despreciables frente a la velocidad de la luz en el vacío c = 3,0.10⁸ ms^-1 . Para velocidades próximas a c será imprescindible un planteamiento relativista del problema.

Dos de las consecuencias que nos interesa destacar aquí son la contracción de la longitud y la dilatación del tiempo.

Se entiende por longitud propia (L₀) de un objeto la que mide para él un observador (S) que lo vea en reposo. Así mismo se denomina tiempo propio (Δt₀) entre dos sucesos al intervalo de tiempo transcurrido medido por un observador que los vea suceder en el mismo punto, es decir, sin velocidad.

Otro observador (S’) que mida longitudes y tiempos para objetos y sucesos que lleven velocidad relativa v con respecto a él medirá para ellos otros valores (L y Δt) que podemos llamar impropios o relativistas:  L es menor que la longitud propia y Δt mayor que el tiempo propio. Apreciaría una contracción longitudinal en la dirección de v y una dilatación temporal. Resumiendo, los objetos son más cortos y los sucesos transcurren más despacio si se ven en movimiento que si se observan en reposo.

La discrepancia entre los valores propios y relativistas de longitudes y tiempos vienen determinados por un factor g según las expresiones que se muestran a continuación. Como se puede apreciar en ellas,  los efectos relativistas de contracción del espacio y dilatación del tiempo sólo son significativos cuando la velocidad v es comparable a la velocidad de la luz, haciendo así que el factor γ  sea claramente mayor que 1.

 

L = L₀ / γ           Δt = Δt₀ . γ         

γ = 1 / √ (1- v²/c²)

Hay que insistir en que los postulados de la relatividad especial y sus conclusiones sólo son válidos para observadores inerciales, es decir no sometidos a fuerzas netas y cuyo movimiento relativo es en línea recta a velocidad constante. Y recordar que los efectos relativistas, en los que ya no es aplicable la mecánica clásica newtoniana, sólo son apreciables cuando la velocidad se acerca al valor límite de la velocidad de la luz.

Como se puede ver, frente al dicho popular según el cual la teoría de la relatividad dice que “todo es relativo”, lo cierto es que la teoría se basa en dos entes invariantes y absolutos: la formulación de las leyes de la mecánica y la velocidad de la luz. Esto es precisamente lo que hace relativa e interdependiente la propia naturaleza del espacio y del tiempo, entrando en conflicto con la idea “de sentido común” de un espacio y un tiempo absolutos e independientes. Pero no pasa nada, tengamos en cuenta que el sentido común ha sido moldeado inconscientemente por la evolución biológica y cultural  de nuestra forma de pensar a lo largo de la historia y nunca ha tenido en cuenta velocidades comparables a la de la luz, distancias cósmicas o diferencias de tiempo infinitesimales. En algunos casos está bien dejarnos guiar por él para asuntos de “andar por casa”, pero ya no sirve para sincronizar relojes atómicos, medir distancias interestelares o investigar partículas subatómicas en movimiento. 

La paradoja de los gemelos es una consecuencia de la discrepancia en la duración temporal de un suceso (el viaje) que surge al aplicar la Teoría de la Relatividad Especial, vista desde dos sistemas de referencia distintos (el viajero y el que espera en Tierra) 

 

Volvamos pues con la paradoja de los gemelos

Supongamos dos hermanos gemelos, Ulises y Penélope. Cuando ambos cumplen 30 años, Ulises se embarca en  un largo viaje de ida y vuelta  hasta la estrella Ítaca que se encuentra a una distancia de 24,5 años-luz de la Tierra, mientras que Penélope se queda en la Tierra esperando su regreso. La nave en la que viaja Ulises hace su larga travesía a la enorme velocidad  de 0,98 c, es decir, al 98 % de la velocidad de la luz. La pregunta es: ¿cuánto habrá durado el viaje y qué edad tendrán los dos gemelos cuando vuelvan a encontrarse?

La proximidad a la velocidad de la luz, nos obliga a hacer el cálculo empleando la teoría de la relatividad, según la cual los espacios y tiempos propios vienen afectados por un factor γ = 1 / √ (1- v²/c²) en función del observador que los mida. Para este caso concreto, v = 0,98 c ,  γ = 5,0 

 

Nivel  Inicio. La paradoja de los gemelos tal como algunos la suelen contar.

Consideremos la duración del viaje como el intervalo de tiempo transcurrido entre dos sucesos que son la partida y la llegada que tienen lugar en el mismo punto para ambos hermanos, y que puede ser medido por un reloj en Tierra y otro a bordo de la nave.

Para Penélope, que se ha quedado en la Tierra, el tiempo que han marcado su relojes tanto mecánicos como biológicos (su tiempo propio) para la duración del viaje es lo que ha tardado la nave en recorrer una distancia d de 49 años-luz (24,5 de ida y 24,5 de vuelta) con velocidad v = 0,89 c,  es decir: Δt = d / v =  49 c / 0,98 c  = 50 años

Mientras tanto, Penélope ve que Ulises se desplaza con una velocidad v con respecto a ella, y razona acertadamente que los relojes mecánicos o biológicos que viajan con Ulises, que marcan el tiempo propio de éste Δt₀ , y por tanto el transcurso de su vida, atrasan o se ralentizan con respecto a los de la Tierra, que marcarán un tiempo Δt mayor (el tiempo propio de Penélope), según la expresión relativista: Δt = Δt₀ .γ  ,  En este caso Δt₀ = 50 /5,0 = 10 años, que es el tiempo que para Ulises ha durado el viaje.

En resumen, que cuando se produce el reencuentro en la Tierra, Penélope que ha pasado 50 años de su vida esperando, tendrá 80 años de edad, mientras que su hermano gemelo Ulises, que asegura haber estado 10 años de viaje, tendrá sólo 40 años de edad ¡sería 40 años más joven que su gemela!. Paradójico ¿no?

Es preciso señalar que no es que Ulises haya pasado ese tiempo sumido en una especie de aletargamiento o viviendo como en una película a cámara lenta al estilo de Matrix. De hecho, si eligiésemos a Ulises como marco de referencia, veríamos que el mecanismo de su reloj y su vida a bordo transcurren a ritmo normal, con su tiempo propio.

Vale, hasta aquí la famosa paradoja de los gemelos tal como se suele contar por ahí adelante, incluyendo algunos libros de texto de física. Esto en realidad no es una paradoja y no supone ningún problema. Al fin y al cabo estas discrepancias en el transcurso del tiempo se pueden observar todos los días en los laboratorios de física de partículas con otros “gemelos” no humanos, como las partículas subatómicas, cuyo tiempo de vida media resulta ser significativamente mayor en movimiento que en reposo, y es utilizado normalmente en la sincronización de los relojes idénticos de los satélites de GPS y de la Tierra para ajustar correctamente nuestra ubicación. En cualquiera de los casos, se emplean las ecuaciones de la relatividad especial descritas, y los distintos tiempos obtenidos por cada observador  para un mismo par de sucesos son exactamente iguales a lo que predice la teoría.

 

Nivel Pro. La verdadera paradoja de los gemelos.

Pero el problema de verdad surge si ahora planteamos el viaje desde el punto de vista de Ulises en su nave.  Esto parece perfectamente lícito ya que, al igual que su hermana, es un observador inercial y según la teoría, las mismas leyes físicas se cumplen indistintamente desde uno u otro sistema.

Ulises se vería a sí mismo en reposo y observaría a la Tierra, a su hermana y al entorno cósmico moverse a la misma y tremenda velocidad constante de 0,98 c. Esto no tiene que parecernos extraño, en realidad todo se mueve de una manera u otra dependiendo del sistema de referencia que lo observe. Sólo que la distancia recorrida ya no sería la longitud propia L₀ = 49 años-luz establecida desde la Tierra, sino que estaría contraída según la ley relativista  L= L₀ / γ ,  en un factor γ = 5,0 hasta ser L = 9,8 años-luz para Ulises. Y esto le lleva tan sólo un tiempo de 10 años, que es justo lo que había previsto Penélope para su hermano mientras ella esperaba durante 50 años de su vida. Hasta aquí todo bien.

Pues ahora viene lo bueno. Ulises aplica  Δt = Δt₀ .γ   para hallar el tiempo que ha pasado para Penélope durante sus 10 años de viaje. El tiempo vivido por Penélope es ahora el tiempo propio Δt₀, pues para ella no se ha movido del sitio, mientras que los 10 años de viaje contados por Ulises son el tiempo relativista Δt, pues ve cómo Penélope se ha movido con velocidad.

Si para Ulises el viaje ha durado Δt = 10 años, para Penélope han sido Δt₀ = Δt / γ = 10 / 5,0 = 2 años. Al final del viaje, Ulises tendrá 40 años y Penélope 32.

 Desde el punto de vista de Ulises, el tiempo pasa más despacio para Penélope y en consecuencia, cuando se reencuentren ¡Penélope será más joven que él!. Es la conclusión opuesta al razonamiento planteado desde la referencia de Penélope.

He aquí la auténtica paradoja de los gemelos. Una situación absurda que parece no tener solución.

Y ahora ¡cuidado!. Algunos libros de texto atajan erróneamente diciendo que si, según Penélope, ella cumple 80 años cuando se encuentra a Ulises cuando éste  cumple 40; entonces, igualmente a Ulises le sale que cumple 80 mientras su hermana cumple 40. El cálculo no es correcto, como acabamos de ver.

 

Nivel Premium. La paradoja tiene solución, así que no hay paradoja.

Entonces ¿cuál de los dos gemelos tiene la razón? ¿quién es finalmente el más joven, y cuánto más?. ¿Hay alguna salida para desmontar esta paradoja?. La respuesta es afirmativa y se encuentra en la propia teoría de la relatividad.  Todo parte de  una suposición incorrecta que habíamos pasado por alto, y es que los sistemas de referencia de cada hermano en realidad no pueden ser equivalentes, ya  que es imposible que  se produzca el reencuentro si el gemelo viajero no acelera al salir, da la vuelta en algún momento y frena al llegar, es decir, que sufra aceleraciones. La premisa de que los dos hermanos son sistemas de referencia inerciales y simétricos en el espacio y el tiempo ya no es válida pues el viajero no es inercial en algunos momentos del viaje.

Tanto la teoría como la experimentación coinciden al demostrar que el tiempo se habrá dilatado para el que viaja, con lo que cuando se encuentren otra vez el más joven va a ser Ulises, y la diferencia de edad es la que corresponde al cálculo realizado desde el sistema de referencia inercial de la Tierra. Veamos, esta vez sin cuentas, cómo se puede llegar a esta conclusión que va a suponer la solución de la paradoja.

La teoría de la relatividad general, propuesta por el mismo Einstein 10 años después para extender la relatividad a todo tipo de sistemas de referencia, tanto inerciales como acelerados,  predice que un observador inercial detectará una dilatación del tiempo entre dos sucesos que tengan lugar en un sistema de referencia acelerado o sometido a un campo gravitatorio (dos situaciones equivalentes y físicamente indistinguibles). A pesar de la diferencia de gravedad con la Tierra, las aceleraciones a las que tendría que someterse Ulises para conseguir alcanzar y perder después su altísima velocidad, explicarían según la relatividad general que sea el tiempo propio de Ulises el que haya pasado más lentamente que el de Penélope. Esta idea desmonta la validez del argumento que había empleado el gemelo viajero, deshaciendo así la paradoja.

 

Pero a la misma conclusión se puede llegar sin abandonar el marco de la teoría de la relatividad restringida.

Los dos observadores, aunque supuestamente inerciales, no son simétricos. Penélope está en lo cierto en todo momento pues su sistema de referencia no cambia en ningún momento. Pero Ulises, aun admitiendo que cambie instantáneamente el sentido de su movimiento, invierte en ese instante su sistema de referencia, rompiendo la simetría que hasta ahora mantenía con el otro planteamiento. El cálculo demuestra que asumir ese cambio de referencia  supone que el tiempo observado para Penélope, que según él pasaba más despacio, habría aumentado 48 años de golpe, que sumados a los 2 de ida de vuelta harían los 50 de Penélope, frente a los 10 de Ulises.   

En cualquier caso, para el gemelo que viaja, el tiempo se dilata según el factor g previsto por el que se queda. Como resultado, cuando se produzca realmente el reencuentro de los gemelos, Ulises tendrá 40 años y Penélope 80. El tiempo de Ulises habrá transcurrido γ = 5 veces más lento que el de Penélope. El resultado es único y por lo tanto no hay paradoja.

 

Pero, ¿y si el viajero no acelera ni cambia de sentido en ningún momento?

Por ejemplo, pasando a velocidad v constante y en línea recta al lado del que espera en reposo, o bien cruzándose ambos en movimiento rectilíneo y uniforme en sentidos opuestos con velocidad relativa v.

En este caso los dos sistemas de referencia son inerciales y totalmente equivalentes para las leyes de la relatividad especial. Cada uno ve como su tiempo propio transcurre con normalidad mientras concluye que es al otro al que le pasa más despacio. ¿Otra vez la paradoja? En realidad no. No es una situación paradójica porque, al no poder reencontrarse de nuevo, nunca podrán confrontar entre ellos  ni sus relojes ni el paso de sus vidas a no ser que alguno frene y se pare y vuelva a acelerar ( ya no sería inercial) o se intercambien señales periódicas para comparar sus relojes.  Dichas señales no serían instantáneas, pues como mucho viajarían a la velocidad de la luz, y recorrían una distancia en un tiempo. Estos espacios y tiempos también son interdependientes y relativos al observador, y están sometidos a los mismos efectos relativistas descritos antes. En todo momento los sucesos ocurridos en la situación de cada observador tienen lugar en puntos diferentes del espacio-tiempo y la noción intuitiva de simultaneidad deja de tener sentido.

En conclusión. No hay ninguna posibilidad real de encuentro ni de sincronización de la información del tiempo, así que el problema de los gemelos que se reencuentran no puede plantearse en la realidad. Si no hay problema, no hay paradoja.

 

Referencias y más información:

P. Tipler, G. Mosca. Física para la Ciencia y la Tecnología. REVERTÉ. VI ed. (2015)

H. Young, R. Freedmann. Sears. Zemansky - Física Universitaria con Física Moderna.Vol.2. PEARSON EDUCACIÓN. XII ed. (2009)

J. I. Illana. “Descubre la relatividad”. D. Física Teórica. Universidad de Granada. (2017)  https://www.ugr.es/~jillana/SR/sr.pdf

Javier Santaolalla. Date un Voltio. “La paradoja de los gemelos ¡resuelta!“ https://www.youtube.com/watch?v=lPEo0wDiU0c